Bütünler açı nedir, kaç derecedir? Bütünler açı konu anlatımı

Açılar, geometri alanındaki önemli konulardan biridir. Birden çok açı türü vardır. Ölçüsü 0 derece ile 90 derece arasında olan açılara, dar açı denir. 90 derecelik açılara dik açı adı verilir. 90 ila 180 derece arasında ölçüsü bulunan açılara, geniş açı denir. 180 derecelik açı ise doğru açı diye adlandırılır. 360 derecelik açıya, tam açı adı verilir. Bütünler açı ise, toplam dereceleri 180 olan iki farklı açıya denir. Yani toplam ölçüsü 180 derece olan iki açı, birbirini bütünleyen açılardır.

BÜTÜNLER AÇI KONU ANLATIMI

İki farklı açının ölçüleri toplandığında ortaya çıkan toplam ölçü 180 derece ise, bu iki açıya bütünler açılar denir. İki bütünler açı, aynı zamanda birbirine komşu ise, yani aynı noktadan çıkan ışınlardan oluşuyor ve kendilerini oluşturan ışınlardan biri her ikisi için ortak ise, bu açılara komşu bütünler açılar denir.

BÜTÜNLER AÇI KAÇ DERECEDİR?

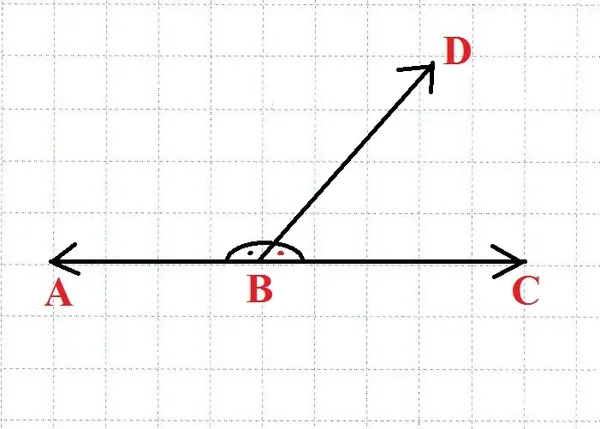
Bütünler açıların, sabit ve standart bir ölçüsü bulunmamaktadır. İki açıyı bütünler açı yapan yegâne kural, bu iki açının ölçüleri toplamının 180 derece olmasıdır. Toplamı 180 dereceyi bulduğu sürece, iki açının ölçülerinin kaç olduğunun bir önemi yoktur. Bütünler açının ölçüsü kaç olursa olsun, önemli olan toplam ölçünün 180 derece olmasıdır. Örneğin, 100 derecelik bir açının bütünleri, 180 – 100 = 80 derece olacaktır.

BÜTÜNLER AÇILARIN TRİGONOMETRİK ORANLARI

Bütünler açıların, trigonometrik oranları vardır. Yani bütünler açıların sinüs ve kosinüsleri arasında belli trigonometrik oranlar söz konusudur. Bütünler açıların ölçülerinin sinüsleri birbirine eşit; kosinüs, tanjant ve kotanjantları ise birbirinin ters işaretlisidir.

• sin(x) = sin(180 – x)
• - cos(x) = cos(180 – x)
• - tan(x) = tan(180 – x)
• - cot(x) = cot(180 – x)