Limit Konu Anlatımı - Parçalı Fonksiyonun ve Mutlak Değer Fonksiyonunun Limiti Nasıl Alınır, ve Kuralları Neler?

Limit konu anlatımı, fonksiyonların belirli noktalardaki değerlerini açıklamayı sağlar. Limit alma kuralları öğrenildiği takdirde işlem yapmak kolaylaşır. Limit nedir sorusuna kısaca verilecek yanıt ise bunun fonksiyon limiti olduğudur. Herhangi bir fonksiyondaki değerler, farklı bir seviyeye ulaştığında fonksiyon grafiğinde değişiklikler meydana gelir. Parçalı fonksiyonun ve mutlak değer fonksiyonun limiti nasıl alınır? İşte detaylar…

Limit Nedir?

Bu kavramın kelime anlamına bakıldığında sınır ve uç nokta anlamına geldiği görülür. Latince, "limes" ve "limites" sözcüklerinden dilimize geçmiştir. Matematikte limit, herhangi bir fonksiyondaki x değerlerinin, ulaşacağı sayıyı ve buna bağlı olarak değişen fonksiyon grafiğinin anlaşılmasını sağlar. Örneğin, herhangi bir sayının çarpımsal tersini veren bir fonksiyon ele alındığında bu, f(×)=1/× olarak gösterilir. Mesela f(x)=1/x fonksiyonu x=0 iken tanımsızdır. X=0 tanımsız olarak kabul edilse bile 0'a yakın olan değerler alınarak x'in sıfıra yaklaştığında fonksiyon grafiğindeki değişimlerin nasıl olacağı gözlemlenebilir.

Yukarıdakine benzer fonksiyonlara "parçalı fonksiyon" adı verilir. Biraz incelendiğinde, x=a noktasında fonksiyonun değiştiğini görmek mümkündür. Bu x=a noktası, f(x) fonksiyonun kritik noktasıdır. X=a noktasının limitinin hesaplanması için sağ ve sol limitlerine bakılmalıdır. F(x) fonksiyonun kritik noktası dışında, diğer herhangi bir nokta için limit hesabı yapılırken söz konusu nokta, parçalı fonksiyona göre yazılacak olan bölümde onun yerine yazılır.

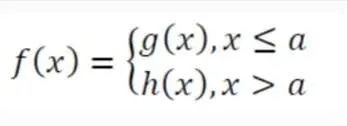
Mutlak değere sahip fonksiyonun kritik noktasındaki limit değerini öğrenmek için parçalı fonksiyondaki yöntem kullanılabilir. Öte yandan, kritik olmayan bir noktadaki limit değerini bulmak için mutlak değer içindeki ifade, bahsi geçen noktadaki değer baz alınarak pozitif ya da negatif işaretli olan mutlak değerden çıkarılır.

Limit Alma Kuralları Nelerdir?

Fonksiyonların limitini bulmak için kullanılan bazı formüller bulunur. Bunlar şu şekilde gösterilir:

Çarpma: limx↦a[f(x).g(x)]=L.M

Bölme: limx↦a[f(x)/g(x)]=L/M

Sabit sayı ile çarpma: limx↦a[kf(x)]=kL

Toplam - fark: limx↦a[f(x)±g(x)]=L±M

Kuvvetler: limx↦a[f(x)]n=[limx↦af(x)]n=Ln

Kökler: limx↦af(x)−√n=limx↦af(x)−√n=L1n