Silindirin Alanı Nasıl Bulunur? Silindirin Kesit ve Yüzey Alanı Hesaplama Formülü Nedir?
Silindir, çok boyutlu geometrik cisimlerden biridir. Geometrinin konularından birisi olan silindir, sınavlarda sıklıkla karşımıza çıkan geometrik cisimler arasında yer almaktadır. Silindir ile alakalı olarak genelde alan ve hacim hesaplama soruları çıkmaktadır. Bu nedenle silindirin alanını hesaplamayı bilmek önemlidir. Peki silindirin alanı nasıl bulunur? Silindirin kesit ve yüzey alanı hesaplama formülü ile birlikte, aşağıda tüm cevapları bulabilirsiniz!

Üstüvane olarak da bilinen silindir, çok boyutlu geometrik bir cisimdir. Tabanları birbirine eş ve olan iki daireden oluşan silindirin yan yüzeyi dikdörtgenlerle kapalıdır. Silindir bu açıdan temel iki geometrik şeklin birleşmesi ile oluşmaktadır. Silindirin tabanlarını birleştiren doğruları bulunmaktadır. Eksenin durumuna göre ise silindir isim almaktadır. Silindirin yüzey alanı hesaplanması için bilinmesi gereken bazı değerler vardır.
SİLİNDİRİN YÜZEY ALANI HESAPLAMA
Daire şeklindeki iki parçanın birbirine paralel olarak tüm kenar noktalarından birleştirilmesi ile silindir şekli elde edilmektedir. Silindirin yanal yüzeyi bir dikdörtgenden oluşmaktadır. Bir silindirin üst ve alt tabanlarını birleştiren dik doğru parçası silindirin yüksekliğini meydana getirmektedir. Görüleceği üzere silindir iki ayrı geometrik şeklin bir araya gelmesi ile oluşmaktadır. Bunu bir şekil ile göstermek gerekirse;
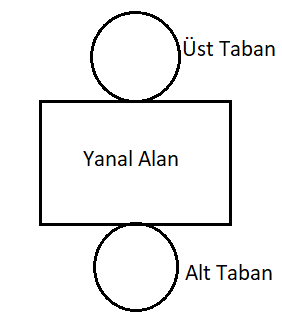
Yukarıdaki şekilden de anlaşılacağı üzere silindirin alanı hesaplanırken, bu iki geometrik cismin alanları ayrı ayrı hesaplanmakta ve çıkan sonuçlar toplanmaktadır. Yani yapılacak işlemler sırasıyla;
1. Öncelikle silindirin alanı hesaplanırken önce taban alanları hesaplanmaktadır. Silindirde iki tane dairesel taban bulunmaktadır. Bu tabanlar birbirine eşittir. Bir dairenin alan formülü π.r2 şeklindedir. Bu formülde "r" birimi dairenin yarıçapını sembolize etmektedir. Bir silindirde iki tane dairesel alan olduğundan; silindirin taban alanları 2 π.r2olarak hesaplanmaktadır.
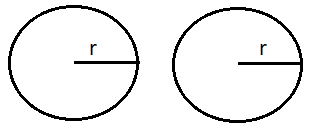
İki dairenin toplam alanı= 2 π.r2
2. Silindirin yanal yüzeyinin bir kenarı, silindirin taban alanının çevresine eşittir. Diğer kenarı ise "h" yani yüksekliktir. Silindirin yanal alanını hesaplamak için öncelikle dairenin çevresini bulmak gerekmektedir. Bir dairenin çevresi 2πr formülü ile bulunmaktadır. Yani 2πr yanal yüzey olan dikdörtgenin bir kenarının uzunluğudur. Dikdörtgenlerin alanları kenar ile yüksekliğin çarpımı ile bulunmaktadır. Yüksekliğe "h" dersek; silindirin yanal yüzeyi olan dikdörtgenin alanı 2πr ile h'ın çarpımı ile bulunacaktır.
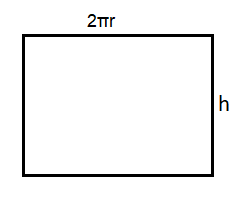
Silindirin yanal alanı= 2πrh
3. Silindirin tüm alanını bulmak için ise son adım, elde edilen iki veriyi toplamaktır. Yani dairelerin alanı ile dikdörtgenin alanını toplamak. O halde silindirin alan formülü 2 π.r2+ 2πrh olarak ifade edilebilir.
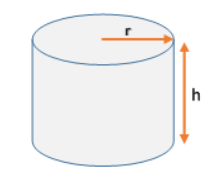
Silindirin tüm alanı= 2 π.r2+ 2πrh
SİLİNDİRİN KESİT ALANI HESAPLAMA
Silindirin kesit alanı, silindirin taban alanına eşittir. Silindirin taban alanı ise bir daireden oluşmaktadır. O halde silindirin kesit alanını bulmak için yapılması gereken tek şey, dairenin alanını bulmaktır. Bir dairenin alanı π.r2 formülü ile hesaplanmaktadır. Burada π sabit bir sayıyı ifade ederken, "r" ise dairenin yarıçapını ifade etmektedir. O halde silindirin kesit alan formülü π.r2 ile bulunmaktadır.
