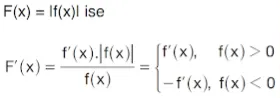Türev Konu Anlatımı - Bileşke Fonksiyonun, Bölümün, Çarpımın Türevi Formülü ve Kuralları
Ortaöğretim son sınıf matematik konuları arasında yer aldığından dolayı birçok öğrenci, türev konu anlatımı hakkında detayları öğrenmek ister. Türev alma kuralları, fonksiyonlara göre değişkenlik gösterir. Türev nedir diyenler için bu kavram, matematikte diferansiyel denklemler ile ilgilidir. Peki bölümün türevi kuralı ve çarpımın türevi formülü nedir? Bileşke fonksiyonun türevi nasıldır?

Türev konu anlatımı, mantığı anlaşıldıktan sonra rahatlıkla kavranabilir. Türev nedir diye merak edenler için bu, bir fonksiyonun limiti bir reel sayı ise söz konusu değer f fonksiyonunun türevidir. Temelde değişimi ölçmek için yararlanılan türev alma kuralları, ezberlenmesi gereken formüllerdir. Bölümün türevi kuralı ve çarpımın türevi formülü, işlem yapabilmek açısından önemlidir. İşte bileşke fonksiyonun türevi ve daha fazlası ile ilgili detaylar…
Türev Nedir?
Öğrenciler tarafından anlaşılması en güç matematik konularından biri olan türevin ne olduğu sıkça sorulan sorular arasındadır. Buna göre, reel sayılardan diğer reel sayılara ulaşan tek değişkenli bir fonksiyona bağlı olan bir noktadaki türev, fonksiyonun söz konusu noktadaki teğet doğrusunun eğimine denktir. Yani bir teğetin diğer bir eğriye, x ekseni üzerinden yapmış olduğu pozitif yönlü açıya ait tanjant değerini ifade eder. Genel olarak türev, bir şeyin ne kadar hızlı değiştiği ile ilgilidir. Değişim hızının hesaplanmasını sağlar. Bu kavramın h türevi ve q türevi şeklinde temelde iki tanımı bulunur.
- H türevi tanımına göre bir f fonksiyonunun a noktasındaki türevin limitidir.
- Q türevinde ise {h} sonsuz küçüğü dahil edilmiştir. Sonsuz küçük sayısının artırılmasına ek olarak küçük katı da yükseltilebilir.
Türev Alma Kuralları Neler?
Fonksiyonlarda türevi bulmayı sağlayan bazı formüller bulunur. Örneğin, bileşke fonksiyonun türevi için (gof)'(x) = g' (f(x)).f'(x) formülünden yararlanılır. Diğerleri için ise aşağıdaki formüller kullanılır.
Logaritma fonksiyonunda türev almak için kullanılması gereken formül şu şekildedir:
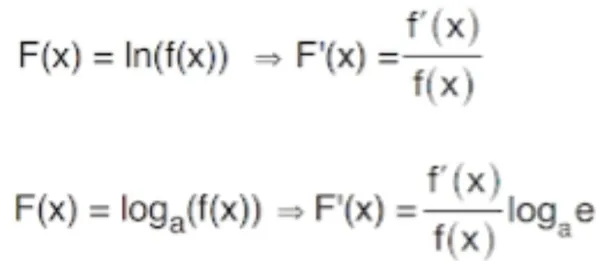
Üstel fonksiyonun türevini almayı sağlayan formül:
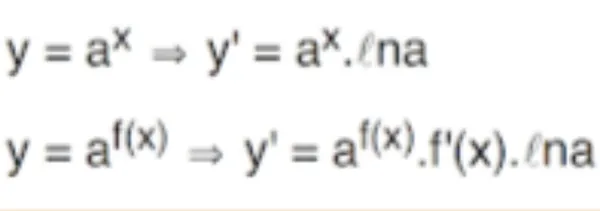
Ardışık türev için uygulanan formül şu şekilde:
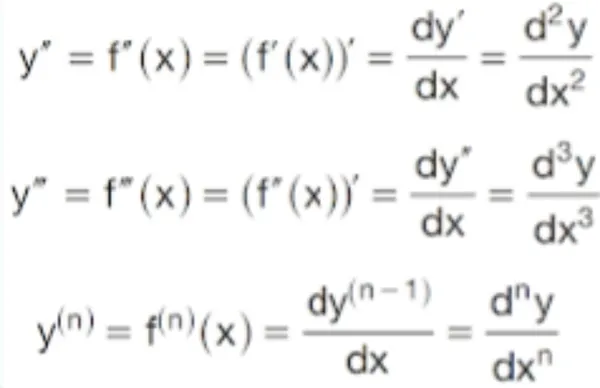
Ters fonksiyonun türevini almayı sağlayan formül:
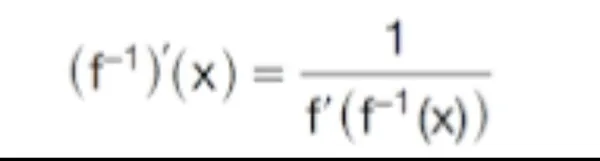
Ters trigonometrik fonksiyonlar için kullanılan formüller şu şekilde:
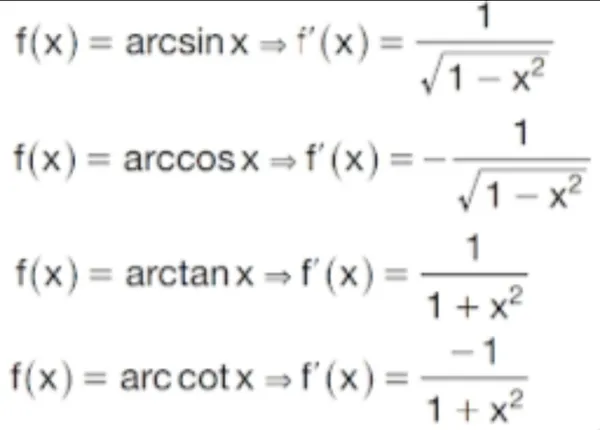
Parametrik denklemlerde ikinci mertebe türev için gereken formüller:
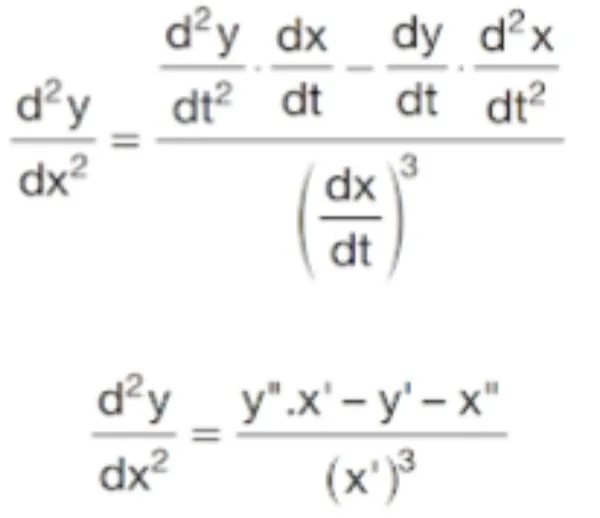
Mutlak değerin türevini almak için ise şu formül kullanılır: